题目
给你一个有 n 个节点的 有向带权 图,节点编号为 0 到 n - 1 。图中的初始边用数组 edges 表示,其中 edges[i] = [fromi, toi, edgeCosti] 表示从 fromi 到 toi 有一条代价为 edgeCosti 的边。
请你实现一个 Graph 类:
Graph(int n, int[][] edges)初始化图有n个节点,并输入初始边。addEdge(int[] edge)向边集中添加一条边,其中edge = [from, to, edgeCost]。数据保证添加这条边之前对应的两个节点之间没有有向边。int shortestPath(int node1, int node2)返回从节点node1到node2的路径 最小 代价。如果路径不存在,返回-1。一条路径的代价是路径中所有边代价之和。
示例 1:
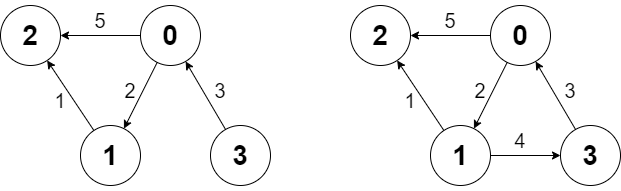
输入:
["Graph", "shortestPath", "shortestPath", "addEdge", "shortestPath"]
[[4, [[0, 2, 5], [0, 1, 2], [1, 2, 1], [3, 0, 3]]], [3, 2], [0, 3], [[1, 3, 4]], [0, 3]]输出:
[null, 6, -1, null, 6]解释:
Graph g = new Graph(4, [[0, 2, 5], [0, 1, 2], [1, 2, 1], [3, 0, 3]]);
g.shortestPath(3, 2); // 返回 6 。从 3 到 2 的最短路径如第一幅图所示:3 -> 0 -> 1 -> 2 ,总代价为 3 + 2 + 1 = 6 。
g.shortestPath(0, 3); // 返回 -1 。没有从 0 到 3 的路径。g.addEdge([1, 3, 4]); // 添加一条节点 1 到节点 3 的边,得到第二幅图。
g.shortestPath(0, 3); // 返回 6 。从 0 到 3 的最短路径为 0 -> 1 -> 3 ,总代价为 2 + 4 = 6 。
提示:
1 <= n <= 1000 <= edges.length <= n * (n - 1)edges[i].length == edge.length == 30 <= fromi, toi, from, to, node1, node2 <= n - 11 <= edgeCosti, edgeCost <= 106- 图中任何时候都不会有重边和自环。
- 调用
addEdge至多100次。 - 调用
shortestPath至多100次。
我的题解
首先要求中增加边和查询的次数在一个数量级上,求最短路径放在查询中和放在更新边中似乎是没什么大区别。如果更新一次边维护一次全局的最短路径,则可以应对更新少查询多的情况,每次addEdge的复杂度:普通Dijkstra是O(n^3),队列优化的Dijkstra是O(n^2*logn),Floyd也是O(n^3);如过更新多而查询少,则每次查询计算单源最短路径更快,每次shortestPath的复杂度:普通Dijkstra是O(n^2),队列优化的Dijkstra是O(n*logn)。
本着够用就行的原则,我选用了Floyd(笑)。
Floyd(On^3)
具体代码如下:
class Graph {
private:
int node_num;
int INF = 1e9+10;
vector<vector<int>> dist;
void update_dist_map(){
// On^3
for(int k=0;k<node_num;k++){
for(int i=0;i<node_num;i++){
for(int j=0;j<node_num;j++){
if(dist[i][j]>dist[i][k]+dist[k][j]) dist[i][j] = dist[i][k]+dist[k][j];
}
}
}
}
public:
Graph(int n, vector<vector<int>>& edges) {
node_num = n;
dist = vector<vector<int>>(node_num+10, vector<int>(node_num+10, INF));
for(int i=0;i<node_num;i++){
// map[i][i] = 0;
dist[i][i] = 0;
}
for(auto e: edges){
// map[e[0]][e[1]] = e[2];
dist[e[0]][e[1]] = e[2];
}
// update dist map
update_dist_map();
}
void addEdge(vector<int> edge) {
dist[edge[0]][edge[1]] = min(dist[edge[0]][edge[1]], edge[2]);
// update dist map
update_dist_map();
}
int shortestPath(int node1, int node2) {
return dist[node1][node2]>=INF?-1:dist[node1][node2];
}
};
/**
* Your Graph object will be instantiated and called as such:
* Graph* obj = new Graph(n, edges);
* obj->addEdge(edge);
* int param_2 = obj->shortestPath(node1,node2);
*/完成时间
2024-03-27
题目链接
https://leetcode.cn/problems/design-graph-with-shortest-path-calculator/
《“2642. 设计可以求最短路径的图类”》 有 1 条评论
牛大逼